这一类问题主要有两种考法,一是求两条已知曲线的公切线,二是由公切线相关的参数范围。
如此如此。
一、求公切线方程
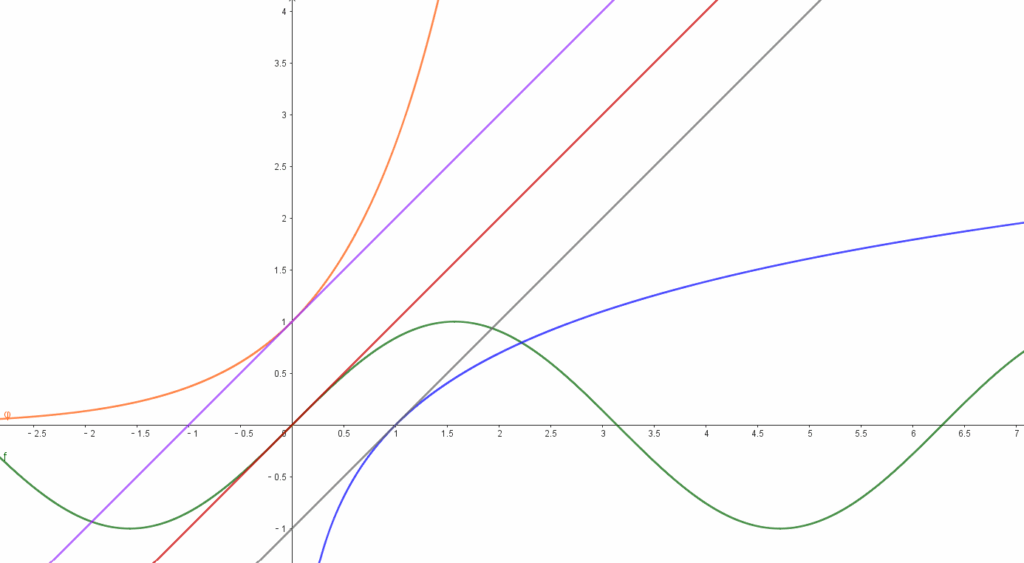
例题1:与![]() 都相切的直线方程?
都相切的直线方程?
析:求解公切线方程在高中阶段最主流的方法是同一法。
即,分别求出这公切线在曲线![]() 上的切点
上的切点![]() ,再利用导数算出斜率,进而表达出
,再利用导数算出斜率,进而表达出![]() 分别在
分别在![]() 的切线
的切线![]() 。最后,通过
。最后,通过![]() 斜率相同,截距相同列出二元一次方程组,最后解出切点坐标,进而求得切线方程。
斜率相同,截距相同列出二元一次方程组,最后解出切点坐标,进而求得切线方程。
(其实这种解法比较繁琐,读者可以找我交流更简单的解法(()
解:设切点:![]()
![]()
则![]()
![]()
两直线斜率相同,截距相同:
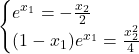
![]()
![]()
所以切线:
![]()
鉴于求解公切线的过程比较繁琐,我推荐记住几个特殊函数在特殊点的切线(毕竟小题很少遇到太恶心人的情况)
![]()
![]()
![]()
主要是为了应对一些比较trivial的小题,就可以在一定程度上简化运算了。举几个例子:
如,求![]() 在点
在点![]() 处的切线:
处的切线:
即将y=x-1向下平移一个单位长度
![]()
这些常用的切线还有大用处(没错,说的就是你,切线放缩.jpg)在这里先按下不谈(?)
我们接下来展示一些实战中的应用:
(全部摘自大橘(凤凰台))
已知![]()
![]()
